> 课例评析

 

 

数学教学通讯

投稿邮箱：sxj***@vip.163***

 

 

 

 

 

 

指向数学核心素养的

“ 教—学—评一致性”的教学实践

——以“反比例函数的图像和性质（第1课时）”为例

 

段有强  王 静

湖南省长沙一中岳麓中学   410205       湖南省长沙长郡梅溪湖中学    410205

 

 

 

 

 

 

《义 务 教 育 数 学 课 程 标 准（2011年 版）》（简称《标准》，下同 ）指出，“数学素 养是 现 代 社 会 每 一 个 公 民 应 该 具 备 的 基本素养，作为促进学生全面发展教育 的重要组成部分，数学教育既要使学生 掌握 现 代 生 活 和 学 习 中 所 需 要 的 数 学 知识与技能，更要发挥数学在培养人的 思维 能 力 和 创 新 能 力 方 面 的 不 可 替 代 的作用”［1］．随着课程改革的持续深化， 如何 提 升 学生的数学核心素养 成 为 广 大一线教师需要思考的问题 ．华东师 范大学崔允漷教授建议“教 —学 —评 一 致性”可“依据清晰的目标处理教材 、选 择方法 ；结合 情 境 创 设 引 导 主 动 的 、反 思式的知识建构；依托学习过程开展参 与式 、嵌入式 的 即 时 评 价 ，为 学 科 核 心 素养 的 课 程 目 标 达 成 指 明 清 晰 的 实 施 路径”［2］.

笔者以“反比例函数的图像和性质

 

（第1课时 ）”为例，探索在教学中如何实 现“教 —学 —评一致性 ”，提高教学的有 效性.

 

研读课程标准，制定学习目标

清 晰 的 目标 是“ 教 —学 —评 一 致 性 ”的 前 提 和 灵 魂 ．没 有 清 晰 的 目 标 ， 就无所谓“教 —学 —评 ”的活动；没有清  晰的目标 ，也 就 无 所 谓 一 致 性 ，因 为 判 断“教 —学 —评 ”是 否 一 致 的 依 据 是 教 学 、学习与评价是否都是围绕共享的目 标 展 开 ．学 习 目 标 的 确 定 需 要 综 合 考 虑课程标准 、教 材 和 学 情 三 个 方 面 ，因 而，笔者确定本节课的学习目标如下.

（一 ）课标研读

《标准》对本部分内容的要求是“能 画出反比例函数的图像，根据图像和表

达式探索并理解k>0和k<0

 

时，图像的变化情况”. （二 ）教材分析

本 节 课 的 主 要 内 容 是 反 比 例 函 数 的图像和性质，反比例函数是继一次函 数 、二次函数学习之后的再一次强化和 拓展 ，图像由“一条 ”到“两 支 ”、形 态 由 “连续”到“间断 ”，是后续构建反比例模 型 解 决 实 际 问 题 的 基 础 ，也 为 高 中 学 习 其他函数做作好了铺垫，起到承上启 下的作用.

（三 ）学情分析

由于学生在八年级下册第十九章 已经学习过一次函数，又在九年级上册 第二十二章学习了二次函数，学生的抽 象思维能力和探究能力都得到了一定 锻炼，基本具备研究函数图像和性质的 思想方法．笔者授课的班级 ，学生基础 一般 ，两极 分 化 比 较 严 重 ，大 部 分 学 生 具备一定的类比研究能力.

作者简介：段有强（1986—），硕士研究生，中学二级教师，曾获得“优秀班主任”“优秀教师”“教研标兵”“市解题比赛一等奖”“市级优课”等荣誉.

 

22 >  2 0 2 2 年 11 月（中旬）

数学教学通讯

投稿邮箱：sxj***@vip.163***

 

> 课例评析

 

（四 ）学习目标

结合课标、教材和学情的分析，基于  学科核心素养，确定本节课的学习目标：

（1）进 一 步 熟 悉“描 点 法 ”作 函 数 图 像的 主 要 步 骤 ，能 画 出 反 比 例 函 数 的图像 ，探 索 并 理 解 图 像的 变 化 情 况 ， 培养学生的动手操作能力，提升直观想 像素养.

（2）类比正比例函数的图像和性质 的研究方法，结合反比例函数的图像，探 究并理解反比例函数的图像和性质，渗 透数形结合 、分 类 讨 论 、从 特 殊 到 一 般 的学习方法，培养学生直观想象和逻辑 推理素养.

（3）能利用反比例函数性质分析并 解决一些基本问题，抓住函数的变化规 律是由k决定 这 一 性 质 ，提 升 学 生 的 数 学运算和逻辑推理素养.

 

依据学习目标，制定评价任务 评 价 任 务 作 为 桥 梁 ，与 目 标 、活 动

相关联 ，它与 目 标 呈 对 应 性 ，并 嵌 入 学 习活动设计之中，保证了三要素的一致 性．评价任务贯穿课堂教学的始终 ，是 学生如何学习 、学到什么程度的判断依 据［3］．学 习 目 标 设 定 之 后 ，应 设 计 用 于 判断目标是否达成的评价任务，评价任 务 的 设 计 优 先 于 教 学 活 动 的 设 计 ，即 “逆向设计”.

评价任务 1 通过 “活动1 ”复习引 入 ，复习的 内 容 都 是 为了“活 动2”作 图 做准备，引导学生正确画 出反比例函数 的图像并理解图像特征，针对目标（1）.

评价任务2“活动3”“活动4”“活动5 ” 环节，通过小组合作学习的方式探究得 到反比例函数的性质，针对目标（2）.

评价任务3“活动6”环节，通过5个 练习题，有梯度地对掌握反比例函数的 图像和性质进行巩固练习，逐步实现知 识向能力的转化，针对目标（3）.

 

依据学习目标，设计教学活动

评价任务的设计先于教学活动的 设计，教师在设计教学活动的时候可以 嵌入评价任务，把评价任务作为教学活 动 的 主 要 组 成 部 分 .  教 师 可 以 这 样 理 解，教学活动同时也是评价任务的呈现 与实施，学习活动同时也是评价任务的 理解与完成［4］.

（一 ）温故知新，引入新知 活动1：

问题 1. 什么叫作反比例函数 ？ 反 比例函数自变量x、函数值y的取值范围 分别是什么？

问题2. 正比例函数的图像和性质 （图表略）.

问题3. “描点法 ”作函数图像的 一 般步骤是什么？

设 计 意 图 通 过 提 问 ，引 导 学 生 复 习 反比例函数 的 相 关 知 识 ，问 题 1中强 调 自变量x和函数值y的取值范围 ，是为 后面画函数图像列表取值不能取0和理 解图 像 为 什 么不 能 与坐 标 轴 相 交 做 好 铺垫． 问题2中回顾了 正比例函数的图 像和性质 ，在 后 续 的图 象 研 究 过 程 中 ， 学生通过类比正比例函数的研究方法， 自然地通过分类讨论（k>0和k<0）来 研 究反比例函数的性质，这也是知识的 一 种正向迁移.

（二 ）观察探究，形成新知 活动2：

问题1．作反比例函数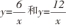

的图像.

图像是直观描述和研究函数的重 要工具，正确画出反比例函数的图像是 研 究 函 数 性 质 的 前 提 ．虽 然 学 生 有 用 “描点法”作一次函数 、二次函数图像的 经验，但是由于反比例函数图像具有自 身的特殊性，大部分学生能够自己准确 画 出 完 整 图 像 的 可 能 性 比 较 小 ．为 了

 

合理安排时间，奇数组学生完成y=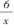的 图像 ，偶数组学生完成y=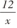的图像．在

“列 表 ”这 一环节 ，由于活动 1复习了反 比例函数自变量x的取值范围 ， 这里学 生很少出现取0的情况．在“连线 ”这 一 环节中 ，学 生 可 能 存 在 以 下 问 题 ：未 用 光滑的曲线 连 接 ，连 线 有 端 点 ，将 两 个 象限内的点连起来等，笔者通过实物投 影将学生的问题汇总展示 ．学生很难 理解图像无限接近坐标轴，但不与坐标   轴相交，在活动1中强调自变量x和函数值 y的取值范围 ，这 也 为 学 生 提 供 了“数 ” 的 角 度 的 理 解 .  笔 者 再 通 过 几 何 画 板   展示两个函数的图像，帮助学生从“形 ” 的角度直观理解，体现数形结合思想.

问题2．反比例函数y=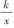 ，k取不同

的正数时，图像有怎样的特点？

笔 者 通 过 几 何 画 板 ，变 化 正 数k的 取值 ，让学 生 直 观 感 受 图 形 的 变 化 ，渗 透它的形态特征.

活动3：

观 察 反 比 例 函 数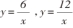 ， y= 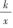（k>0）的图像，能得到哪些特征？

笔者采取小组合作的形式，小组内  合理分工，领导者 、记录者 、汇报员等分 工协作，高效地完成了反比例图像的理 解和性质的研究．在小组合作过程中 ， 教师观察每组的完成情况，对于有问题 的小组进行指导，对因基础差而不愿参 与的学生进行鼓励，对于顺利完成的小 组提出表扬，引导已经形成结论的小组 与其他小组进行组间交流．小组合作结 束后，派代表上台利用实物投影进行展 示，有异议的地方由其他小组进行补充［5］. 学生在描述图像变化趋势时，教师一定 要强调“在每一象限内”这个条件.

2 0 2 2 年 11 月（中旬）<  23

> 课例评析

 

 

数学教学通讯

投稿邮箱：sxj***@vip.163***

 

活动4：

当k<0时 ，反比例函数y=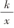的图像

和性质是怎样的呢？请画出反比例函数

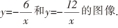
笔 者 安 排 奇 数 组 完 成y=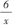－ 的 图 像 ，偶数组完 成y=－的 图 像 ，通 过 再

次画反比例函数的图像，不仅能巩固和 提高学生的作图能力，而且学生在画图 过程中能直观理解k<0时反比例函数的 性质 ．笔者通过实物投影展示几位学 生的作图，对容易出错的地方进行强调. 笔者通过几何画板，变化负数k的取值， 让学生直观感受它的形态特征 ．学生 类比k>0时的图像性质 ，很自 然 地 能 说 出k<0时的图像性质.

活动5：

总结反比例函数y=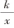（k≠0）图 像

的特征和性质，填写表1. 表1

 

函数		图像	分布象限	增减性
y= 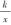（k≠0）

设计意图  反比例函数图像和性质 的探索对于学生来说难度比较大，笔者 先让学生独立思考作图，亲身经历作图 的过程，更好地理解图像所反映出的性 质特征．在探究反比例函数的性质时 ， 笔者采取小组合作的方式，组内分工 合 作，基础弱一些的学生也能被带动参与 其中，对团队讨论出来的结论的印象会 更加深刻 ，这 样 课 堂 更 高 效 ，也 能 培 养 学生的 团队协作能力.

（三 ）巩固提高，运用新知

活动6：

问题 1．下列图像中是反比例函数

图像的是 .

 

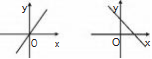
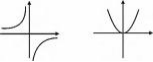A．                        B. y y

x

O O x

C． D.

问 题 2．如 图 1所 示 的 图 像 对 应 的

函数解析式可能是 .

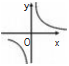
图1

A．y=5x B．y=2x+3

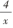C．y= D．y=-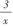

问题3．填空

（1）函 数y=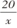 的 图 像 在 第 _______

象 限 ，在 每 一 象 限 内 ，y随 x的 增 大 而

（2）函数y=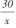－的图像在第_______

象 限 ，在 每 一 象 限 内 ，y随 x的 增 大 而

（3）函数y= ，当x>0时 ，图像在第

象限，y随x的增大而 .

问题4．已知反比例函数y= ，

（1）若 函 数 图 像 位 于 第 一 、三 象 限 ，则k_______；

（2）若 在 每 一 象 限 内 ，y随x的 增 大

而增大，则k .

问题5．已知反比例函数的图像经 过点A（2，6），

（1）这 个 函 数 的 图 像位 于 哪 些 象 限 ？y随x的增大如何变化？

（2）点 B（3，4），C（－2，6）是 否 在 这 个函数图像上？

（3）若D（x1，y1），E（x2，y2）都在这个 反 比 例 函 数 图 像 上 ，且x1 >x2 >0，那 么y1

 

和y2有怎样的大小关系？

（4）若点P（x，y）在这个反比例函数 图像上，当x>3时，求y的取值范围 .

设计意图  笔者通过选取具有代表 性 、由 易到 难 的 题 目 ，引 导 学 生 在 研 究 每一个问题的特点时，能够紧扣“性质 ” 进行分析，达到理解并掌握性质的 目标.

（四 ）归纳反思，深化新知

本节课我们学习了哪些知识？用到 了什么思想方法 ？ 你有哪些收获？

设计意图  笔者引导学生归纳总结 本节课的知识要点和思想方法，使学生 对 反 比 例函 数 的图 像 和 性 质 有 更 全 面 的认识.

 

结语

“教—学—评一致性”是有效教学的 基本原理 ，能 够 从 本 质 上 解 决“为 什 么 教”“教什么 ”“怎样教 ”“教到什么程度 ” 的教学基本问题．在教学中践行“教 —   学 —评一致性 ”理念，教师的教 、学生的   学以及课堂的评要以学生为中心，围绕 学习目标来展开，使得课堂更加生动高 效，促进学生数学核心素养的提升 .

 

参考文献：

［1］ 中 华 人 民 共 和 国 教 育 部 .  义 务 教 育 数 学课程标准（2011年版）［S］. 北京：北京 师范大学出版社，2012.

［2］ 崔允漷，夏雪梅.“教—学—评一致性”： 意义与含义［J］.  中小学管理，2013（01）： 4-6.

［3］ 李 忻 洁 .  教 —学 —评 一 致 性 教 案 的 编 制 研 究［D］. 山 东：山 东 师 范 大 学 硕 士 学位论文，2019.

［4］ 张菊荣 . “教 —学 —评一致性 ”：从方案 设计到课堂实施［J］. 江苏教育，2017（04）： 29-31.

［5］ 王 静 ，段 有 强 .  基 于“教 —学 —评 一 致 性 ”的 实 践 探 索 —— 以“对 数 函 数 及 其 性质（第 1课时 ）”为例［J］. 中学数学教 学参考，2021（06）：14-16.