案 例 剖 析


 122
122  ANLI POUXI
ANLI POUXI
基于同题异构设计“教—学—评”一体化初中数学分层作业
◎余高霞 ( 甘肃省定西市临洮县椒山初级中学,甘肃 定西 743000)
【 摘要】在初中数学教学中,分层教学是一种有效 的教学方法,可以满足不同学生的学 习 需求.文章 以 “ 同题异构”为理论基础,探讨 了 基于“ 同题异构”设 计“教—学—评”一体化的初中数学分层作业的可行 性和有效性.通过对实际案例的设计和实施,收集并分 析相关数据,基于优等生、中等生和学困生的不同基 础,设计相应的作业形式.不同的作业形式可使不同层 次学生达成自 己的学习目标,使数学作业分层设计更 加科学,从而提升数学作业效果.
【 关键词】同题异构;“ 教—学—评”一体化;初中 数学;分层作业
初中阶段学生有着明显的个体差异,如何让不同 能力的学生均能通过数学作业提升数学水平是值得 研究的问题.“ 教—学—评 ”一体化就是实现 教 学 内 容、学习内容和考核指标的统一,其对分层作业的实 施具有重要意义.
一、案例设计
( 一)知识点选择:人教版初中数学八年级上册 “ 三角形全等的判定”
作为初中数学的一部分,“三角形全等的判定”在 数学知识体系中占据重要位置.它为学生打下了理解 几何学的基础,帮助学生初步掌握几何图形的性质和 关系.全等的概念和判定是几何学中最基础和最重要 的知识之一.学习“三角形全等的判定”能够帮助学生 建立起几何观念,形成对几何图形的认识和直觉感.
( 二)样本选择和分层方式
本案例选择八年级某班学生为样本,该班共有 46 名学生,男生 26 名,女生 20 名.该班级在整个八年 级中处于中上水平,具有较强的代表性.在分层方式 上,本案例依据学生的数学成绩将学生划分为优等 生、中等生、学困生三个类别.其中 优 等 生 选 取 班 级 数学名次前十的学生,学困生选取班级数学名次后十 的学生,其他学生归为中等生.
( 三)案例目标
优等生 |
中等生 |
学困生 |
1 . 熟练掌 握 三 角 形全等的基本概 念,能 够 对 三 角 形全等的判定条 件进行推导. 2. 能够利 用 三 角 形全等的判定条 件进行简单的问 题 解 答,包 括 判 定两个三角形是 否全等以及推导 出 三 角 形 全 等 所需的条件. 3. 能够运 用 三 角 形的全等性质解 决相关的实际问 题,如 计 算 三 角 形的边和角 |
1 . 了解 三 角 形 全 等的基本概念和 判定条件. 2. 能够 正 确 使 用 三角形全等的判 定条件判断两个 三角形是否全等. 3. 能够 利 用 已 知 信息推导出三角 形全等所需的条 件,并 进 行 简 单 的证明. 4. 能够 应 用 三 角 形全等的知识解 决较简单的实际 问题 |
1 . 掌握基本的三 角 形 全 等 的 概 念,理 解 三 角 形 全 等 的 判 定 条件. 2. 能够正确运用 给定的判定条件 判断两个三角形 是否全等. 3. 能够简单地应 用三角形全等的 知识解决一些基 本的实际问题 |
( 四)案例流程
1 . 学生“学”的部分
对于初中数学“ 三角形全等的判定”这一章节的 内容,优等生、中等生和学困生可以采取不同的学习 方式,以达到各自的学习目标.
优等生 |
中等生 |
学困生 |
1 . 自 学 教 材:可 以 仔 细 阅 读 教 材,并 多 次 阅 读 相关定理的证明 过程,以加深理解. 2. 拓展学习资源: 可以使用网络资 料,寻找更多关于 |
1 . 关注重点:重点 关注教材中关于 三角形全等的基 本概念和判定条 件,理 解 基 本 的 定理和证明过程. 2. 学习经典例题: 查阅经典例题的 |
1 . 阅 读 教 材:可 以 仔 细 阅 读 教 材,理 解 三 角 形 全等的基本概念 和判定条件. 2. 刷 题 巩 固:可 以选择适合自己 水平的练习题,逐 |

续 表
优等生 |
中等生 |
学困生 |
三角形全等的知 识,了 解 更 多 定 理和应用场景, 熟悉全等三角形 的应用案例. 3. 解决挑战问题: 可以主动解决 一 些复杂的问题, 挑战自己的思维 和应用能力. 4. 交流讨论:与其 他优秀的同学进 行 讨 论,分 享 学 习 心 得 和 解 题 方法. |
解题 过 程,加 深 对判定条件的理 解 ,分 析 解 题 思路. 3. 观看视频教程: 结合 教 材,观 看 一些相关的教学 视频,以 辅 助 理 解和记忆. 4. 解决实际问题: 尝试应用所学的 知识解决一些实 际问 题,加 深 对 三角形全等的应 用意义的理解 |
步 提 高 解 题 能 力,多提问,及时 纠正错误. 3. 寻 求 帮 助:及 时向老师或同学 请教,在 学 习 中 遇到 困 难 时,寻 求帮 助 和 指 导, 及时解决问题. 4. 反 复 强 化:通 过反复复习和练 习,巩 固 基 础 知 识 ,提 升 学 习 能力 |
2. 教师“教”的部分
在教师讲解知识之前,学生已经通过自学的方式 对该章节知识点有了一定的了解.因此,教师在“ 教 ” 的过程中只需要根据学生的学习情况,开展针对性教 学即可.
(1) 针对优等生
教师可为优等生提供更高层次的拓展学习资源, 如复杂问题、实际应用情境等,以满足他们对知识深 入理解和应用的需求.教师可向优等生提供学习案例, 鼓励优等生进行独立研究和探究,使之深入思考并提 出自己的解决方法,培养其创造性思维能力.教师还可 组织学习小组,让优等生之间进行交流,分享学习心 得,激发彼此之间的互相学习和竞争意识.
(2) 针对中等生
教师可详细讲解三角形全等的基本概念和判定 条件,确保中等生能够理解并掌握重点知识.教师可通 过实物演示加深中等生对全等三角形的理解.教师还 可通过解题示范,演示如何运用判定条件,引导中等 生掌握解题思路与技巧.针对中等生的水平,教师可进 行差异化教学,根据难易程度分层讲解,并设计不同 难度的练习题,帮助中等生逐步提升.
(3) 针对学困生
教师可重点讲解三角形全等的基本概念和简易 判定条件,帮助学困生建立起扎实的基础.教师可设计 相关习题帮助学困生巩固知识记忆和技能运用,帮助 其提高解题能力.针对学困生的具体问题和困难,教师 还可进行个别辅导和指导,帮助他们理解和解决难点.
此外,教师需要根据学生的学情和学习进度合理
案 例 剖 析

安排课堂活动,如小组合作学习、游戏探索等,以激发 学生的学习兴趣和积极性.同时,教师需要不断关注学 生的学习进展,及时给予反馈和指导,鼓励学生思考 和自主学习,促进他们在学习过程中成长和进步.
3. 分层作业评价
针对学困生设计了以下基础类题目:
1 . 如图 1 , 已知△ABC≌△ADE , AB = AD , BC= DE , 那么与∠BAE 相等的角是 .
2. 如 图 2 , 已 知 △ABC ≌ △AED , AE = AB , ∠E -
∠D = 20 ° , ∠BAC= 60 ° , 求∠C 的度数.
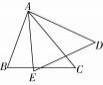
图 1 图 2
3. 如图 3 , 将 直 角 △ABC( 其 中 ∠B = 34 ° , ∠C = 90 ° ) 绕 A 点按顺时针方向旋转到△AB ′ C ′ 的位置,使 得点 C , A , B ′ 在 同 一 条 直 线 上,那 么 旋 转 角 最 小 等 于( ) .
A . 56 ° B . 68 ° C . 124 ° D . 180 °
4. 如 图 4 , △ACB ≌ △A ′ CB ′ , ∠BCB ′ = 30 ° , 则 ∠ACA ′ 的度数为( ) .
A . 20 ° B . 30 ° C . 35 ° D .40 °
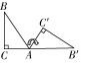
图 3 图 4
针对中等生设计了以下提高类题目:
1 . AD 为△ABC 中 BC 边上的中线,若 AB = 2 , AC = 4 , 则 AD 的范围是( ) .
A .AD<6 B .AD>2
C . 2<AD<6 D . 1<AD<3
2. 已 知 在 △ABC 中,AD 平 分 ∠BAC , 且 ∠C = 2∠B , 求证:AB = AC+CD.
3. 如图 5 , 在△ABC 中,AB = AC , 延长 AB 到 D , 使 BD = AB , 取 AB 的 中 点 E , 连 接 CD 和 CE. 求 证: CD = 2CE.
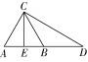
图5
案 例 剖 析


 124
124  ANLI POUXI
ANLI POUXI
4. 如图 6 , 在 △ABC 中,∠C = 2 ∠B , ∠ 1 = ∠2. 求 证:AB = AC+CD.
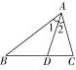
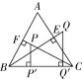
图 6 图 7
针对优等生设计了以下挑战类题目:
1 . 如图 7 , 在锐角三角形 ABC 中,BE , CF 分别是 AC , AB 边上的高,BE 延长至 Q , 使 BQ= CA. 在 CF 上取 点 P , 使 CP= BA , 分别沿 Q 和 P 点向 BC 作垂线,垂足 为 O ′ , P ′ , 求证:PP ′ +QQ ′ = BC.
2. P 为正方形 ABCD 对角线 BD 上任意一点,沿着 P 点分别 向 BC 和 CD 上 作 垂 线,垂 足 为 E , F , 连 接 EF , 求证:AP= EF.
3. 如何利用剪刀、白纸、量角器制作出两个全等三 角形?
4. 思考生活中的全等三角形应用情况,分析全等 三角形在生活中的应用案例.
二、案例结果和讨论
( 一)分层作业的设计和实施效果分析
在该案例中通过针对不同层次学生设计分层作 业,在很大程度上提升了各层次学生的学习积极性.对 于优等生来说,给他们提出了更高难度的挑战,激发 了他们的求知欲望和探索能力.对于中等生来说,给他 们提供了难度适中的练习和巩固机会.中等生可以在 适合自己水平的作业中巩固、掌握基本知识和方法, 并逐步提高自己的能力,他们能够在较为自信和舒适 的环境下进行学习,可提升学习动力和自信心.对于学 困生来说,给他们提供了更低难度的起点,帮助他们 逐步掌握基础知识和方法.学困生可以在简单的题目 中逐渐建立自信和对数学学习的兴趣,通过小步快跑 的方式逐渐迎头赶上.各层次学生作业完成情况如下 表所示.
|
平均正确率( % ) |
完成时长 |
优等生 |
80 |
30 分钟 |
中等生 |
80 |
35 分钟 |
学困生 |
80 |
33 分钟 |
( 二)学生对“ 同题异构”作业的反馈和评价
对于优等生来说,他们对这种作业设计的反馈通

常是非常正面的.这是因为对于他们来说统一难度的 作业可能无法充分发挥他们的才智和能力.而“ 同题 异构”的作业设计,可以使他们面对更加复杂和有挑 战性的问题,促使他们深入思考,提升解题能力,从而 获得满足感和成就感.
对于中等生来说,他们通常能够在适宜难度的作 业中找到学习动力.这种作业设计能够帮助他们巩固 和应用所学的知识,使他们逐步提升解题技巧.中学生 在完成这些作业的过程中能够体会到 自 己的进步和 成长,增强数学学习信心.
对于学困生来说,他们常常面临学习上的困难和 挫折.“ 同题异构”的作业设计可以使他们接触到相对 简单和入门级的题目,从而巩固基础.这种分层作业设 计能够帮助他们建立学习的起点,减少焦虑感,从而 激发起他们对数学学习的兴趣.
结 语
在本 案 例 中,首 先 对 学 生 进 行 了 层 次 划 分,这 为科学地开展“ 教”与“ 学”奠定了基础.“ 学”的部分 采用了学生自学为主、教师引导为辅的方式,为不同 层次的学生提供了丰富的教具,激发了学生的学习热 情.“教”的部分根据学生的学习 目标不同,采取了不 同的形式( 异构),优等生的实践环节更多,思维深度 也更深,学困生则更加侧重基础.在“评”的环节,主要 采用习题作业的方式来检验学生的学习效果,不同层 次学生的平均正确率均为 80% , 说明题目难度设计合 理,能够激发不同层次学生的学习热情.因此,教、学、 评三个 环 节 处 于 同 一 平 面 上 才 能 够 发 挥 其 应 有 的 价值.
【 参考文献】
[1] 孔佳蕾.基于学生发展的初中数学分层作业
设计与实施[ J] . 智力,2023(25) :108- 111 .
[2] 白永潇.核心素养视角下的初中数学分层作
业设计[ J] . 新课程教学( 电子版),2023(10) :1 - 3 .
[3] 任丽莎.基于“ 双减”政策的初中数学分层作 业设计策略研究[ J] . 教学管理与教育研究,2023 ( 9) :
71 - 73 .
[4] 冯俊,王芳.基于定边对定角模型的同题异构
[ J] . 中学数学,2022(2) :75- 76 .
[5] 李大为.同题异构 点亮智慧的火花:2011 年 江苏省初中数学青年教师评优课“ 圆”的设计亮点评
析[ J] . 中学数学杂志,2012( S2) :44-46 .